今天在看《Filthy Rich Clients》时看到一个画星星的程序片段,忽然就打算看自己能不能写出这个程序来。最初以为没有难度,到真正写起来又不知如何下手,无奈就在纸上画起了图。嗖嗖,半个小时过去了,基本上有了想法,先把星星尖角的点算出来再说。这个不就是圆内接正多边形的接点吗,我的想法很直接,就是先给一个初始点,然后作圆心到这个点的线段,然后把线绕圆点转按一定的角度,得到的新线段的点就是星星新的尖角。如此循环直到所有星星的点出来为止。说的不明白,上图先:

OK,准备动手写,可线段这么旋转呢,既然说自己写就不能用AffineTransform了。无奈又在纸上嗖嗖画了起来,良久,终于发现我对三角函数的认识退步到a=sin(a)*c的水平。最后还是用我这个水平逼出一条等式出来,但我居然单纯地以为两条线都是在第一象限中,出来的图形自然乱七八糟。这时彷佛陷入绝境了,突然灵光一现记起有个东西叫向量,向量是什么东西我还是知道的,但那些运算法则都忘光光了。在我那堆书里翻了翻找到一本有几页讲向量的书,这是一部关于游戏人工智能的书,里面对向量的介绍仅仅是概念上的层面。不过点乘的介绍还是给我带来曙光。立刻上维基,里面对向量还真简洁,不过数量积、向量积的内容还是挺可观的,看了许久感觉没什么帮助,又转战三角函数页面,基本把各个恒等式跟定理都回忆了一遍。期间还手贱点了某网站,看了不少八卦新闻。回过神来才发现整个晚上的时间都快没了,可这条线段怎么旋转貌似还没找到解决办法?就在把尘封多年的十年高考拿出来之际,一个名词又在脑海中浮现——极坐标。马上上维基
一看心里暗爽。
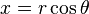
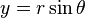
我要的不就是这两条式子吗,如今怎么简洁的摆在眼前怎么能不兴奋。什么线段旋转啊都不用。直接就可以求出旋转后的点。这里再仔细说明一下一个圆内接的n角星星的尖角点就是这个圆的内接正n边形的接点,而圆的内接正多边形的内角是相等,且内接正n边形每条边对应的圆心角都等于360°,这个角度也就是星星中相邻的两个点旋转的角度,为了方便我也把它称为这个星星的圆心角。那么现在求星星的尖角点也就很简单了,给出一个圆,一个初始点,然后依次加上圆心角并代入公式,就可求出所有点了。但是就算把所有尖角点连起来也就是个正多边形,星星在哪里呢?其中我在第一次嗖嗖地画图时就发现,画一个完美的星星其实就是一个大圆的内接n边形和另一小一点的同心圆的内接n边形,两个内接n边形的角度偏转是它的边对应的圆心角的一半,然后依次把每个顶点连接起来就OK了。好像又是不明不白的表述,再上图:



既然如此一个内接多边形已经出来了,离星星还会远吗?于是乎我就嗖嗖地编起了代码。
Java语言: 一個生成星星形狀的GeneralPath方法
/**
* 一個生成星星形狀的GeneralPath的方法
* @param x0 星星外接圓的圓心
* @param y0 星星外接圓的圓心
* @param r 外接圓的半徑
* @param v 這個怎么這么說呢,決定星星的胖瘦吧,取值(0,1)
* @param baseRadian 決定星星的角度,弧度來的
* @param branchescount 星星的角數
* @return
*/
public static GeneralPath justStar(double x0,double y0,double r,double v,double baseRadian,int branchescount){
double d = 2*Math.PI/branchescount;
double [][] p = new double[branchescount*2][2];
for(int i = 0; i<p.length ;i++){
p[i][0]=x0+r*Math.cos(i/2*d+baseRadian);p[i][1]=y0+r*Math.sin(i/2*d+baseRadian);
i++;
p[i][0]=x0+v*r*Math.cos((i/2+0.5)*d+baseRadian);p[i][1]=y0+v*r*Math.sin((i/2+0.5)*d+baseRadian);
}
GeneralPath path = new GeneralPath();
path.moveTo(p[0][0], p[0][1]);
for(int i=1 ; i<p.length ;i++){
path.lineTo(p[i][0], p[i][1]);
}
path.closePath();
return path;
}
到此总算告一段落了,整整一个晚上都在画星星,好像小学生。能聊以安慰的是总算复习了一下向量跟三角函数,这下应该能记住一段时间了。突然想起有次校内的ACM比赛有道水题,考的是用海伦公式求三角形面积,我居然把海伦公式给忘了,并为此推导许久,还推不出来。赛后我就暗下决心一定要把海伦公式记住,想不到现在又想不起来了。杯具啊,觉得再写一遍
\(p=(a+b+c)/2;\) \(S = \sqrt{p(p-a)(p-b)(p-c)}\) 一定要把它记住。
确实,才发觉有些东西要写出来才印象深刻,于是乎就有了这篇文章,不过不用又会很快忘记。